I have a problem with the prevailing style on Wikipedia. It is cumbersome and exclusionary.
We all recognize Wikipedia’s style.
The problems are:
- The descriptions are unrecognizable even when the subject is familiar.
- Statements contain many complex words or concepts which have to be unpacked and cross-referenced.
- Advanced mathematics and graphs add confusion instead of clarity.
These problems make it difficult to learn about the subject.
I would like to see editors make their writing more accessible rather than more academic.
For example, I admire Hemingway
[Hemingway] relied on the [The Kansas City] Star’s style guide as a foundation for his writing: “Use short sentences. Use short first paragraphs. Use vigorous English. Be positive, not negative.”
and the advice Lawrence Krauss and Neil deGrasse Tyson give in one of their conversations.
Neil deGrasse Tyson: The point is if you put all that information up front, you’re losing the other points you’re trying to make. And you are allowed pedagogical approximations. Otherwise, you cannot communicate in any way with someone who doesn’t know anything.
Lawrence Krauss: People depend on … experts to lead them in the right direction: to give them the correct perspective–if not the details–[be]cause the details almost never matter.
Neil deGrasse Tyson: Correct. People don’t know the details don’t matter in most cases.
In my own writing, I pull definitions into the text and build on simple concepts rather than force people to cross-reference.
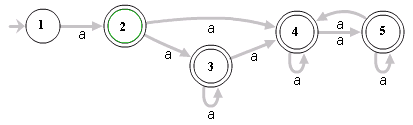
I recently had this issue while looking up “ReDoS” (regular expression denial of service). The first article I read appeared on the OWASP website. But it was written in the style of (if not lifted from) Wikipedia.
There, the article used the words “exponential”, “naïve algorithm”, “nondeterministic finite automaton”, and a state diagram (shown above) as part of the introduction to the subject.
It might be appropriate to add these details later. But the average person won’t understand what these terms mean. And people who otherwise have an interest in the subject will give up.
Have you had trouble reading Wikipedia entries on unfamiliar subjects? What about familiar ones? Were the entries you’ve read as helpful as they could have been?